Feature Detection

We support the definition and systematic detection of complex features based upon a formal topological approach and an algorithmic framework that leverages the theory to permit an effective and accurate data analysis. Our theoretical toolbox combines the classical critical point theory commonly used in fluid dynamics, and combinatorial algebraic topology, which offers guaranteed numerical stability and is robust to non-smooth data. The analysis produces diagrams, measurements, and visualizations that aid understanding intricate structures, provide qualitative domain segmentation, and rank topological features by importance yielding a multi-scale framework within which one can selectively analyze local and global trends in the data. Our direct interaction with the users allows them to formulate their feature characterization hypotheses in terms of this framework and map the corresponding formal, unambiguous definitions to automatic and reliable extraction algorithms. This approach can replace traditional informal characterizations, which are hard to reproduce and less amenable for a systematic and verifiable analysis within a truly scientific method. We are developing:

1. robust tools for computing the topological segmentation of 2D and 3D flows;
2. external memory versions of this computation for large 3D data;
3. algorithms for simplifying topological features;
4. user interfaces for the interactive navigation of topological information;
5. hierarchical models to represent topology at multiple levels of resolution and test interactively adaptive refinement and coarsening of the topological models;
6. geometric approximation with guaranteed error bounds for any given simplified topology;
7. data correlation metrics based on topological trends.

We achieve real time exploration of large regular grids via a novel hierarchical z-order data layout combined with progressive computation of output slices or volume rendering.

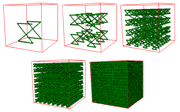
We use the 3D z-order space filling curves to define a hierarchical subsampling of a regular grid.

Simple bit manipulations allow to compute the address of a data sample in hierarchical z-order from the original (i,j,k) row major array index. This allows to combine the coarse-to-fine progressive traversal with fast direct data access.

Practical performance tests show order of magnitude improvement with respect to previous storage layouts and scalability with respect to both data size and computing resources available.